回归模型有很多种,比如最简单的线性回归,还有多项式回归,样条回归等,具体的可以看看这篇介绍:https://blog.csdn.net/tMb8Z9Vdm66wH68VX1/article/details/79922750
简单介绍一下线性回归:
比如,现在广告公司可以投入媒体的营销渠道非常多,从传统的电视,广播,户外这类大众媒体,到电子邮件,短信,电话这种直销媒体,再到现在新兴的各种app以及微信等社交应用所组成的数字媒体。媒体的形式越来越多样化,影响受众行为的方式也日益增多。在商业计划中,我们需要分辨出哪些媒体平台和广告营销活动是最有效的。以销售额为例,假设随着营销变量的逐步增高,销售额也会对应地逐步增高或者减少,不会出现曲线的关系,即为线性回归分析。
保险场景中,用户的保费和赔付金额娱乐场景中,用户的出行次数和度假市场电商环境中,用户网页停留时间以及购物车的商品数量回归分析的结果通常会以y和x之间的方程来描述。
例如,销售额=81521+0.3*电视广告+0.15*社交媒体+0.05*电话直销+0.02*短信推送。
从统计角度解读,81521为截距,表示所有输入都为0时,销售额也能达到的数值0.3等为各个解释变量前的系数,表示其他不变的情况下,电视广告投入每增加一万元,销售额增加三千元从业务角度解读:现实生活中,销售额不会随着广告的投入而直线上升,会呈现边际递减效应,广告投入到一定数额之后,对销售额的影响就会减少,呈现饱和的态势。使用回归模型的结果,最主要的还是观察各个因素系数的大小,横向比较它们对目标变量的关系。
回归分析的结果应该着重于不同x对y的影响对比,而非依赖于线性关系对未来做出非常明确的预测。
下面分享一个利用线性回归模型预测小红书销售额的案例
数据链接:https://pan.baidu.com/s/1Pwcd80BlDFht74GOBBTowg提取码:xw34
销售额为预测目标
数据中各字段的含义:
Rvenue:用户的下单购买金额(预测目标)
3rd_party_stores:用户过往在app中从第三方商家购买的数量,为0则代表只在自营产品中购买
Gender:1为男,0为女,未知则空缺
Age:年龄,未知为空缺
Engaged_last_30:最近30天在app上有参与重点活动(讨论、买家秀等等)
Lifecycle:生命周期分类A、B、C(分别对应注册后6个月内,1年内,2年内)
days_since_last_order:最近一次下单距今的天数(小于1则代表当天有下单)
previous_order_amount:以往累计的用户购买金额
导入pandas和numpy包,导入数据
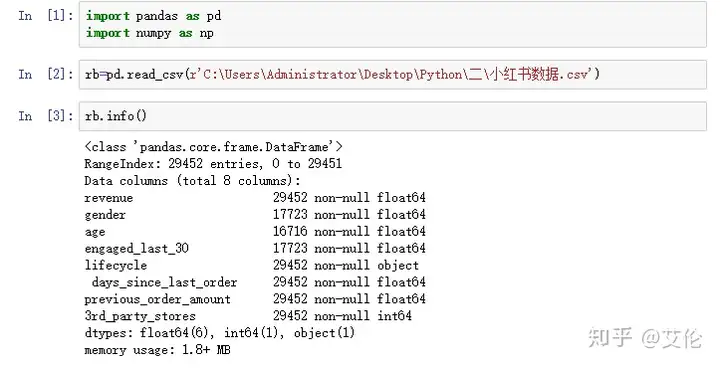
查看空值占比,gender,age,engaged_last_30占比很高
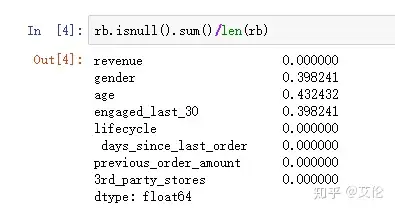
处理缺失值:先处理连续变量,再处理类别变量;连续变量可以用均值,中位数或数据模型填充。
缺失值为连续变量的是‘age’,用均值填充
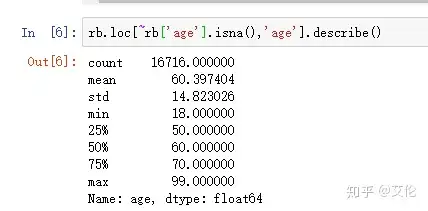
这里‘~’代表否定,查看age中排除缺失值后的数据情况,均值为60.397
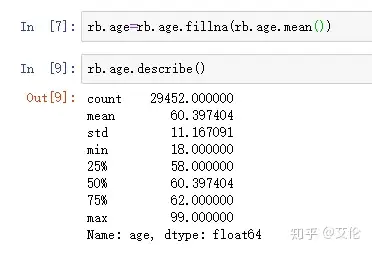
用age缺失值填充‘age’均值
然后处理类别型变量,一般先把类别型变量拆解,然后生成哑变量。gender和engaged_last_30处理方式相同
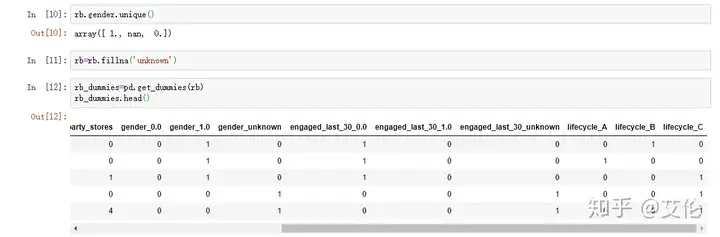
这里gender中存在3种值[0,1,nan],先用unknown填充空值nan,再用get_dummies将其拆解成3个值:gender_0,gender_1,gender_unknown;engaged_last_30也是同理,结果如上图,那这里gender_0为1时则代表为女性。
接下来可以看下各变量相对于revenue的相关性系数
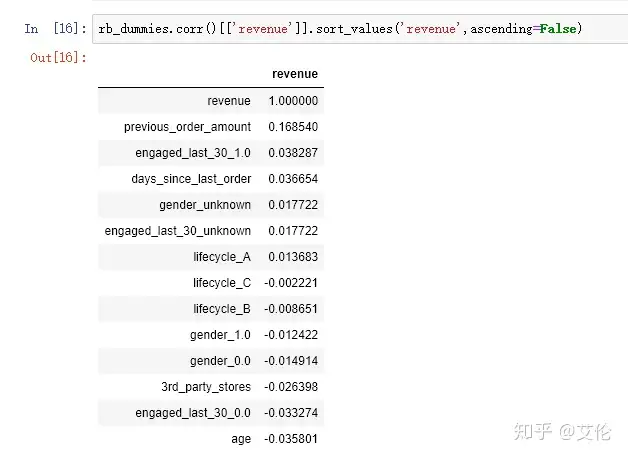
相关系数都不是很大,最大相关性变量是以往累计的购买金额‘previous_order_amount’
用散点图观察一下‘previous_order_amount’和‘revenue’的相关性
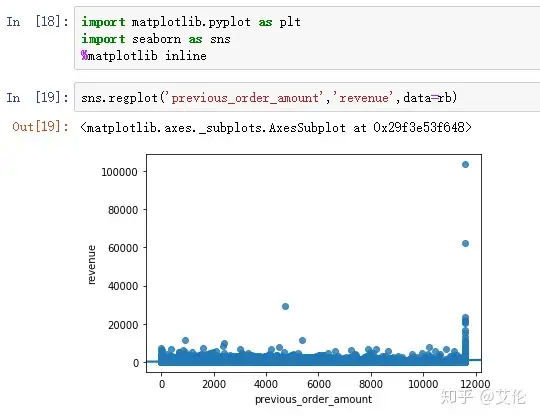
没有呈现出相关性
基于这种情况先尝试一次回归模型
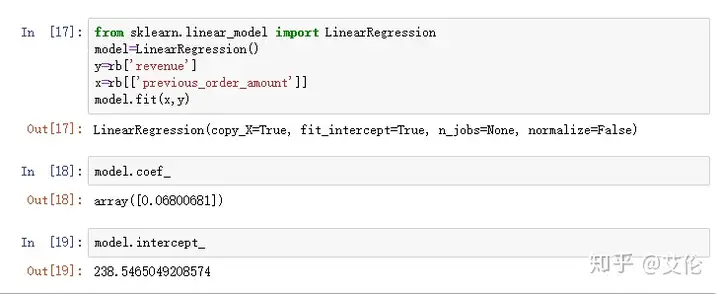
用sklearn.linear_model模块中的线性模型LinearRegression
进行一个单变量分析,因为其他变量和revenue的相关性系数都太小了。
fit(x,y)模型拟合,什么是拟合,我理解为,比如这个线性回归例子,两个变量,那在图上显示就是二维的好多个点,找到一条直线可以正好让这些点在这条线上或者离这条线最近,生成这条线就是fit(x,y)的作用,类似一元线性方程y=kx+c,这里k就是0.06800681,c就是238.5465
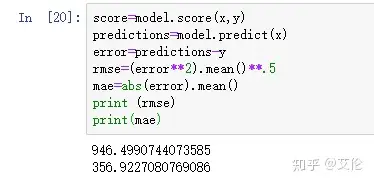
对模型进行评分
predictions=model.predict(x),输入测试数据x,得出预测结果y
误差error=预测结果y-实际y
rmse(均方根误差):均方根误差是预测值与真实值偏差的平方与观测次数n比值的平方根,均方根误差是用来衡量观测值同真值之间的偏差
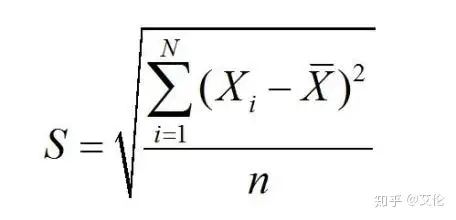
mae(平均绝对误差):也是反映预测值误差的
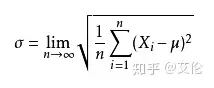
标准模型输出表:
因为这是一元线性回归模型,所以这里用statmodels模块中OLS(最小二乘法)
通过Q的最小来确定这条直线的系数和截距
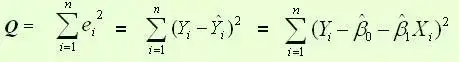
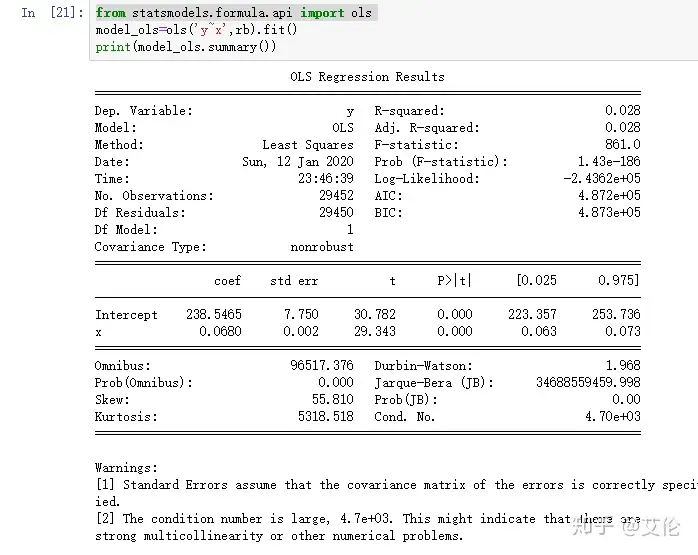

R方特别低,说明模型的解释力度非常弱,这个模型只能解释2.8%的revenue的变化
得到的模型为:revenue=238.5465+0.068*previous_order_amount
预测表示:以往累计的购买金额每增加1000个单位,小红书的销售额就增加68个单位,但是R方非常低,需要寻找更好的模型。
优化模型:
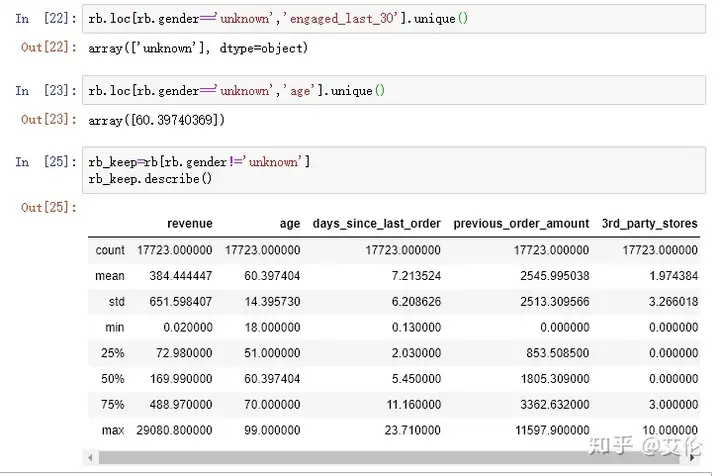
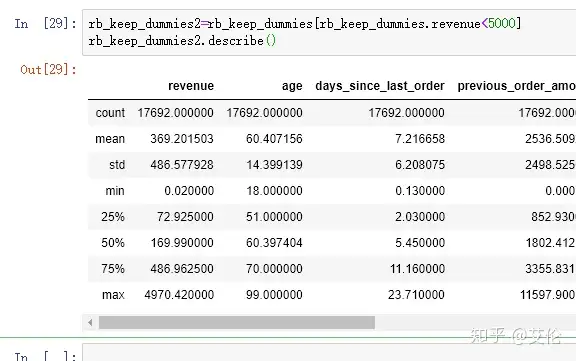
当gender为‘unknown’时,engaged_last_30也为‘unknown’,当gender为‘unknown’时,年龄是用均值填充的60.3974,说明年龄原来也是‘unknown’,也就是gender,engaged_last_30和age这三个包含的缺失值是一致的,可能是系统性偏差,尝试把这部分数据去除后建模。
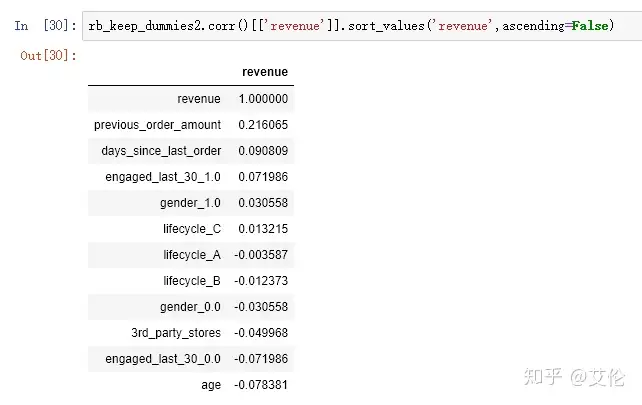
再查看一下对于‘revenue’的相关性
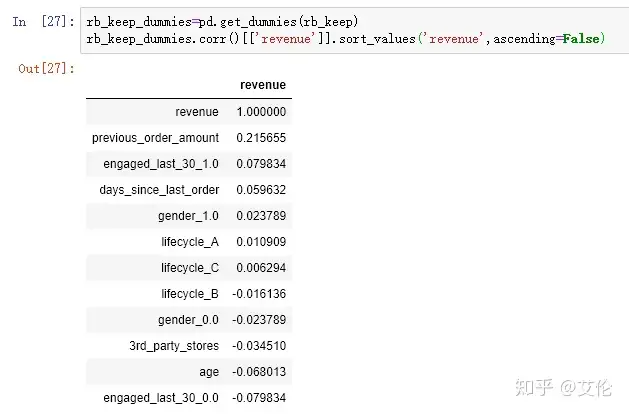
发现previous_order_amount的相关性从原来的0.168540提升到了0.215655
另外从上面describe()中发现revenue的极差很大,max比上四分位数大很多
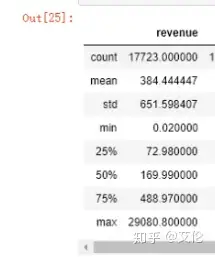
可以利用数据桶看看renvenue的值分布
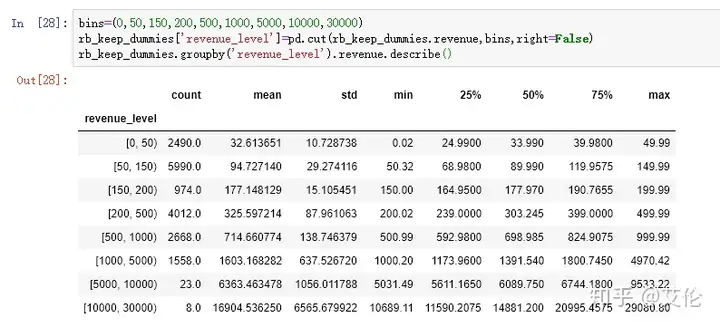
right=False为建左闭右开桶,发现5000以上的数据其实很少,可以剔除
画出对应散点图
可以看出直线有斜率了
重新建立优化模型
R方提升为0.047
如果我们再增加几个变量呢?
将days_since_last_order和age也加入自变量
R方提升至0.064
模型的均方根误差和平均绝对误差都明显减少了
所以新的模型预测方程为:
revenue=338.1638+(previous_order_amount)*0.0433
-(age)*2.3481
+(days_since_last_order)*8.7197
